这篇文章上次修改于 2384 天前，可能其部分内容已经发生变化，如有疑问可询问作者。

定义

• 前序遍历（DLR），是二叉树遍历的一种，也叫做先根遍历、先序遍历、前序周游，可记做根左右。前序遍历首先访问根结点然后遍历左子树，最后遍历右子树。
• 中序遍历（LDR）是二叉树遍历的一种，也叫做中根遍历、中序周游。在二叉树中，先左后根再右。巧记：左根右。
• 后序遍历（LRD）是二叉树遍历的一种，也叫做后根遍历、后序周游，可记做左右根。后序遍历有递归算法和非递归算法两种。在二叉树中，先左后右再根。巧记：左右根。

[以上内容来由于百度百科]

理解

左右不变为前提，“前中后”的方向指“根”的位置，及LR的顺序不变，D在前中后变化。

实现

• 先定义实体类（赋值放在构造函数中在操作时有点乱-_-!）

  public class BinaryTree {
  
      private String name;
      private BinaryTree leftTree;
      private BinaryTree rightTree;
  
      public BinaryTree(String name,BinaryTree leftTree,BinaryTree rightTree){
          this.name = name;
          this.leftTree = leftTree;
          this.rightTree = rightTree;
      }
  
      public String getName() {
          return name;
      }
  
      public BinaryTree getLeftTree() {
          return leftTree;
      }
  
      public BinaryTree getRightTree() {
          return rightTree;
      }
  }

• 造一个数据

  private static BinaryTree create(){
  
  //        return new BinaryTree("A",new BinaryTree("B",null,null),new BinaryTree("C",null,null));
  
          return new BinaryTree("A",new BinaryTree("B"
                  ,new BinaryTree("D",new BinaryTree("F",null,null)
                  ,new BinaryTree("G",null,null))
                  ,new BinaryTree("E",null
                  ,new BinaryTree("H",null,null)))
                  ,new BinaryTree("C",new BinaryTree("I",new BinaryTree("J"
                  ,new BinaryTree("K",new BinaryTree("M",null,null),null)
                  ,new BinaryTree("L",null,null)),null),null));
      }

屡一下这个数据，以图表示：

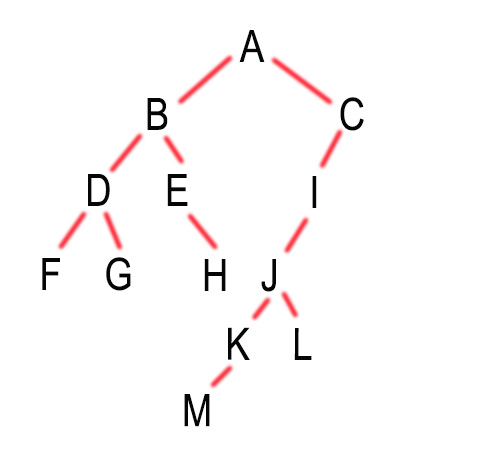
下面，开始对这个二叉树遍历

• 前序遍历

  /**
   * 前序
   * @param tree
   */
  private static void preorder(BinaryTree tree){
  
      if (tree !=null){
          System.out.print(tree.getName()+" ");
          preorder(tree.getLeftTree());
          preorder(tree.getRightTree());
      }
  
  }

• 中序遍历

  /**
   * 中序
   * @param tree
   */
  private static void inorder(BinaryTree tree){
  
      if (tree !=null){
          if (tree.getLeftTree() != null) {
              inorder(tree.getLeftTree());
          }
  
          System.out.print(tree.getName() + " ");
  
          if (tree.getRightTree()!=null){
              inorder(tree.getRightTree());
          }
      }
  
  }

• 后序遍历

  /**
   * 后序
   * @param tree
   */
  private static void postorder(BinaryTree tree){
  
      if (tree !=null){
  
          if (tree.getLeftTree() != null) {
              postorder(tree.getLeftTree());
  
              if (tree.getRightTree() != null) {
                  postorder(tree.getRightTree());
              }
  
              System.out.print(tree.getName() + " ");
  
          }else if (tree.getRightTree()!=null){
              postorder(tree.getRightTree());
              System.out.print(tree.getName() + " ");
          } else {
              System.out.print(tree.getName() + " ");
          } 
      }
  }

• 运行结果

前序：
A B D F G E H C I J K M L
中序：
F D G B E H A M K J L I C
后序：
F G D H E B M K L J I C A

2018/3/5.

Dean.King

Beijing